Information Transmission, Information Storage, Amount of Information.
Let’s understand the following tutorial before diving into the theory:
Tutorial 1: Understanding Fixed-Length vs. Variable-Length Encoding
Scenario:
Consider in a digital commutation channel only four letters A, B, C, and D are transmitted from a transmitter to a receiver repeatedly. But we observed that the probabilities of occurrences of each letter is different and noted as under:
Probabilities of Each Letter:
• A: 50% (0.5)
• B: 25% (0.25)
• C: 15% (0.15)
• D: 10% (0.10)Part 1: Fixed-Length Encoding
In fixed-length encoding, each letter is assigned a code of equal length. With four letters, we use a 2-bit code for each.
Encoding Table for Fixed-Length:
A is assigned to code “00” means 2 bit long code
B is assigned to code “01” means 2 bit long code
C is assigned to code “10” means 2 bit long code
D is assigned to “11” means 2 bit long code
Average = (2+2+2+2)/ 4 = 2 bits per letter
Part 2: Variable-Length Encoding (Shannon’s Method)
In variable-length encoding, we assign shorter codes to more frequent letters. This results in a more efficient encoding scheme.
Encoding Table for Variable-Length:
Letter Probability Encoding Bits
A 50% (0.5) 0 1
B 25% (0.25) 10 2
C 15% (0.15) 110 3
D 10% (0.10) 111 3
Average Bits per Letter Calculation:
• The calculation considers both the probability of each letter and the number of bits used in its encoding:
• (0.5 × 1) + (0.25 × 2) + (0.15 × 3) + (0.10 × 3) = 1.75 bits per letter.Conclusion:
By comparing these two methods, it’s evident that variable-length encoding is more efficient than fixed-length encoding. The average bits per letter in variable-length encoding is 1.75, lower than the 2 bits per letter in fixed-length encoding. This demonstrates how Shannon’s entropy principle can be applied to optimize data encoding for efficiency.
This tutorial illustrates the fundamental principles of data encoding, highlighting the practical application of Shannon’s theory in digital communications and data storage.
Under Development…..
In his landmark 1948 paper, “A Mathematical Theory of Communication,” Claude Shannon introduced the concept of Information Entropy, which laid the foundation for modern information theory.
Here’s an explanation of Information Entropy aimed at non-technical audiences:
Understanding Information Entropy:
1. Basic Concept:
• Information Entropy, often just called ‘entropy’, is a way to measure the ‘surprise’ or ‘uncertainty’ involved in a set of possible outcomes.
• Think of it like a measure of how much you don’t know before you receive a message. The more surprised you are by the message, the higher its entropy.
2. Analogy:
• Imagine a game where you have to guess the outcome of a dice roll. If it’s a regular six-sided dice, your uncertainty is higher than if it’s a dice with three sides marked ‘1’ and three sides marked ‘2’. In Shannon’s terms, the six-sided dice has higher entropy.
3. Importance in Communication:
• In communication, entropy helps us understand how much ‘real’ information is being transmitted. For instance, if you’re receiving a message that’s very predictable (like a repeated ‘hello’), the entropy is low because there’s little new or surprising information.
• High entropy means the message has a lot of new, unpredictable information, which is crucial in efficient communication systems.
4. Quantifying Information:
• Shannon’s theory quantified information mathematically, allowing it to be measured in bits (like how length is measured in meters). This quantification is essential for data compression and transmission.
5. Practical Implications:
• In practical terms, Shannon’s entropy has applications in data compression (like zip files), telecommunications, and cryptography. It helps in designing systems that transmit information efficiently and securely.Key Points to Remember:
• Entropy measures uncertainty or surprise in a message.
• Higher entropy means more uncertainty, and therefore, potentially more ‘new’ information.
• This concept is fundamental in the digital world for things like data storage, transmission, and security.Shannon’s work essentially gave us a way to measure and optimize how we send, receive, and store information in the digital age. It’s a cornerstone of how we understand and handle data in various fields, from internet communication to securing sensitive information.
Key Phrases and Explanations:
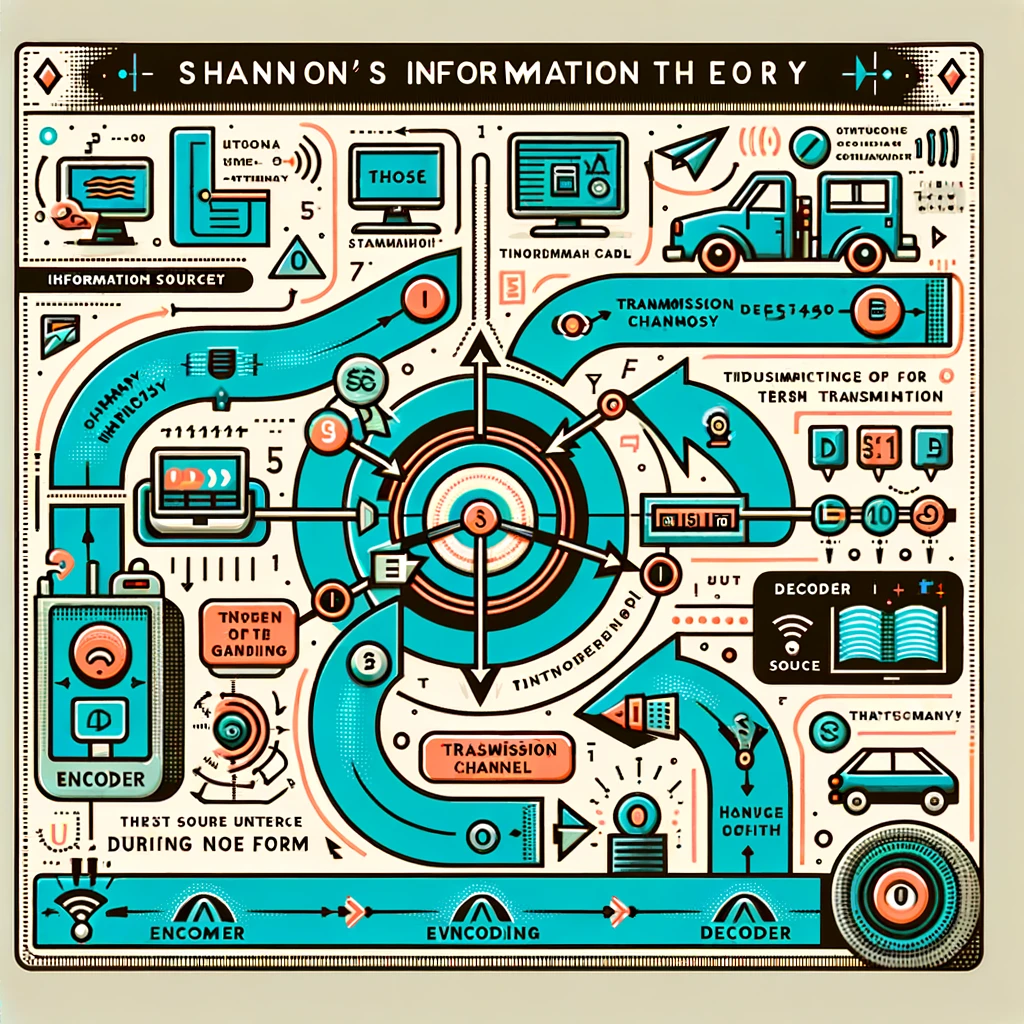
• “Information Source”: Where the message originates.
• “Encoder”: Converts the message into a signal or coded message.
• “Transmission Channel”: The medium through which the signal is sent.
• “Noise Source”: Represents any interference in the channel.
• “Decoder”: Interprets or reconstructs the signal back into a message.
• “Receiver”: The end point where the message is delivered.
Key Concepts:
• “Entropy”: A measure of uncertainty or information content.
• “Redundancy”: Extra bits added to improve reliability of message transmission.
• “Noise”: External factors that distort the clarity of the signal.